PostsPytorchでPhysics-Informed Neural Networkを実装する ②2次元のバーガース方程式
概要
前回の続き。
Physics-Informed Neural Network(PINN)によるバーガース方程式の予測を2次元空間に拡張します。
コード
データセットの作成
データセットをx, yの2次元に拡張します。前回までは扱うデータが時刻t,空間座標x,物理量uの3つだったところが,時刻t,空間座標(x, y),速度ベクトル(u, v)の計5つとなります。
初期条件として,x, yが負のときにu = -sin(x) + 1またはv = -sin(y) + 1に従う速度分布を与えます。境界条件は,x, y座標それぞれの端部で(u, v)=(1, 1)となるようにしました。
# 初期条件: x∈[-1,0], y∈[-1,0], t=0のとき,u=-sin(x), v=-sin(y)
n_initial = 500
t_initial = np.zeros(n_initial)
x_initial = (np.random.random(n_initial) - 0.5) * 2
y_initial = (np.random.random(n_initial) - 0.5) * 2
u_initial = np.ones(n_initial)
v_initial = np.ones(n_initial)
for i in range(n_initial):
if (x_initial[i]<0)&(y_initial[i]<0) :
u_initial[i] = -1 * np.sin(np.pi * x_initial[i]) + 1
v_initial[i] = -1 * np.sin(np.pi * y_initial[i]) + 1
# 境界条件: 壁面で(u, v)=(1, 1)
n_boundary = 250
t_boundary = np.random.random(n_boundary*2)
x_boundary_h = np.random.choice([-1, 1], n_boundary)
y_boundary_h = (np.random.random(n_boundary) - 0.5) * 2
x_boundary_v = (np.random.random(n_boundary) - 0.5) * 2
y_boundary_v = np.random.choice([-1, 1], n_boundary)
x_boundary = np.block([x_boundary_h, x_boundary_v])
y_boundary = np.block([y_boundary_h, y_boundary_v])
u_boundary = np.ones(n_boundary*2)
v_boundary = np.ones(n_boundary*2)
# 支配方程式の残差を評価する計算領域内の座標
n_region = 10000
t_region = np.random.random(n_region)
x_region = (np.random.random(n_region) - 0.5) * 2
y_region = (np.random.random(n_region) - 0.5) * 2
# 可視化
plt.figure(figsize=(4, 3))
plt.scatter(x_initial, y_initial, c=np.sqrt(u_initial**2+v_initial**2), vmin=1, vmax=2.8)
plt.scatter(x_boundary, y_boundary, c=np.sqrt(u_boundary**2+v_boundary**2), vmin=1, vmax=2.8)
plt.colorbar()
plt.show()
速度ベクトル(u, v)の絶対値を可視化してみると,以下のようになります。
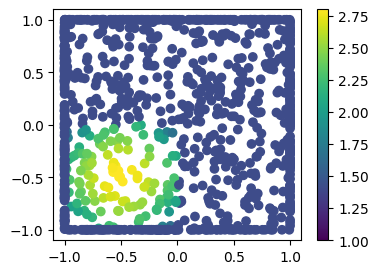
速度ベクトル(u, v)はそれぞれ正の向きの速度を持っているため,紙面の右上に向かって流れが移動することが期待されます。
モデル作成
モデルのクラスを変更します。net_f()関数に書かれている通り,支配方程式がx,yそれぞれの方向の2本となります。その他,次元に合わせてu, x等の変数の中身を書き換えています。
(微分係数の計算のところコードが汚いですね...)
class NN(nn.Module):
def __init__(self, n_input, n_output, n_hiddens=[32,64,128,128,64,32]):
super(NN, self).__init__()
self.activation = nn.Tanh()
self.input_layer = nn.Linear(n_input, n_hiddens[0])
self.hidden_layers = nn.ModuleList(
[nn.Linear(n_hiddens[i], n_hiddens[i+1]) for i in range(len(n_hiddens)-1)]
)
self.output_layer = nn.Linear(n_hiddens[-1], n_output)
def forward(self, x):
x = self.activation(self.input_layer(x))
for layer in self.hidden_layers:
x = self.activation(layer(x))
x = self.output_layer(x)
return x
class BurgersPINN():
def __init__(self, model, nu):
"""
"""
self.model = model
self.nu = nu
def net_u(self, x, t):
""" 物理量を出力
"""
u = self.model(torch.cat([x, t], dim=1))
return u
def net_f(self, X, t):
""" 支配方程式との残差を出力
"""
# モデルが予測する物理量
U_pred = self.net_u(X, t)
u = U_pred[:, [0]]
v = U_pred[:, [1]]
# 微分係数を逆伝搬で計算
du_dt = torch.autograd.grad(u, t, grad_outputs=torch.ones_like(u), retain_graph=True, create_graph=True)[0].T[0]
dv_dt = torch.autograd.grad(v, t, grad_outputs=torch.ones_like(v), retain_graph=True, create_graph=True)[0].T[0]
du_dx, du_dy = torch.autograd.grad(u, X, grad_outputs=torch.ones_like(u), retain_graph=True, create_graph=True)[0].T
dv_dx, dv_dy = torch.autograd.grad(v, X, grad_outputs=torch.ones_like(v), retain_graph=True, create_graph=True)[0].T
du_dxx, _ = torch.autograd.grad(du_dx, X, grad_outputs=torch.ones_like(du_dx), retain_graph=True, create_graph=True)[0].T
_, du_dyy = torch.autograd.grad(du_dy, X, grad_outputs=torch.ones_like(du_dy), retain_graph=True, create_graph=True)[0].T
dv_dxx, _ = torch.autograd.grad(dv_dx, X, grad_outputs=torch.ones_like(dv_dx), retain_graph=True, create_graph=True)[0].T
_, dv_dyy = torch.autograd.grad(dv_dy, X, grad_outputs=torch.ones_like(dv_dy), retain_graph=True, create_graph=True)[0].T
# 支配方程式に代入(f=0だと方程式と完全一致)
fx = du_dt + u.T * du_dx + v.T * du_dy - self.nu * (du_dxx + du_dyy)
fy = dv_dt + u.T * dv_dx + v.T * dv_dy - self.nu * (dv_dxx + dv_dyy)
return (fx + fy).T
def fit(self, X_bc, Y_bc, X_region, max_epochs=300, learning_rate=0.01, pi_weight=5e-4):
""" 学習データでモデルを訓練
"""
# 入力データをスライス
t = X_bc[:, [0]]
x = X_bc[:, [1,2]]
u = Y_bc
t_region = X_region[:, [0]]
x_region = X_region[:, [1,2]]
# 入力をtorch.tensorに変換
t = torch.tensor(t, requires_grad=True).float()
x = torch.tensor(x, requires_grad=True).float()
u = torch.tensor(u, requires_grad=True).float()
x_region = torch.tensor(x_region, requires_grad=True).float()
t_region = torch.tensor(t_region, requires_grad=True).float()
# 最適化ロジック
optimizer = torch.optim.Adam(self.model.parameters(), lr=learning_rate)
# モデルを学習モードに変更
self.model.train()
# 学習
history = []
for epoch in range(max_epochs+1):
# 現在のモデルで予測
u_pred = self.net_u(x, t)
f_pred = self.net_f(x_region, t_region)
# 損失を計算
loss_u = torch.mean((u - u_pred)**2)
loss_pi = torch.mean(f_pred**2)
loss_total = loss_u + loss_pi * pi_weight
# 誤差逆伝搬
loss_total.backward()
# 最適化ソルバーで重みを動かす
optimizer.step()
# 最適化ソルバーの勾配情報を初期化
optimizer.zero_grad()
if epoch % 10 == 0:
print(f'epoch:{epoch}, loss:{loss_total.item()}, loss_u:{loss_u.item()}, loss_pi:{loss_pi.item()}')
history.append([epoch, loss_total.item(), loss_u.item(), loss_pi.item()])
return np.array(history)
def predict(self, X_in):
""" モデルの予測
"""
t = X_in[:, [0]]
x = X_in[:, [1,2]]
# 入力をtorch.tensorに変換
x = torch.tensor(x, requires_grad=True).float()
t = torch.tensor(t, requires_grad=True).float()
self.model.eval() # 評価モードに変更
u = self.net_u(x, t).detach().numpy()
f = self.net_f(x, t).detach().numpy()
return u, f
学習
学習のところはほとんど変わっていません。
今回は時間t,空間座標(x, y)をもとに速度ベクトル(u, v)を予測するネットワークが必要になるので,model = NN(3, 2)のようにしておきます。
# 学習用のデータ
X_bc = np.block([[t_initial, t_boundary], [x_initial, x_boundary], [y_initial, y_boundary]]).T
Y_bc = np.block([[u_initial, u_boundary], [v_initial, v_boundary]]).T
X_region = np.block([[t_region], [x_region], [y_region]]).T
print("shape:", X_bc.shape, Y_bc.shape, X_region.shape)
model = NN(3, 2)
pinn_model = BurgersPINN(model, nu=0.01)
# モデルを学習
history = pinn_model.fit(X_bc, Y_bc, X_region, max_epochs=1000, learning_rate=0.01, pi_weight=0.1)
可視化
以下のコードで,流れの時間変化を見てみます。
# 予測したいポイント
n = 100
x_pred = np.linspace(-1, 1, n)
y_pred = np.linspace(-1, 1, n)
x_grid, y_grid = np.meshgrid(x_pred, y_pred)
fig = plt.figure(figsize=(18, 3))
for i, t in enumerate([0, 0.25, 0.5, 0.75, 1]):
t_pred = np.ones(n*n) * t
X_in = np.block([[t_pred], [x_grid.flatten()], [y_grid.flatten()]]).T
pred,_ = pinn_model.predict(X_in)
u_pred = pred.reshape(n, n, 2)[:,:,0]
v_pred = pred.reshape(n, n, 2)[:,:,1]
# 物理量を可視化
fig.add_subplot(1, 5, i+1)
plt.contourf(x_pred, y_pred, np.sqrt(u_pred**2+v_pred**2), np.linspace(1,3,21))
#plt.colorbar()
plt.title(f't={t}')
plt.show()
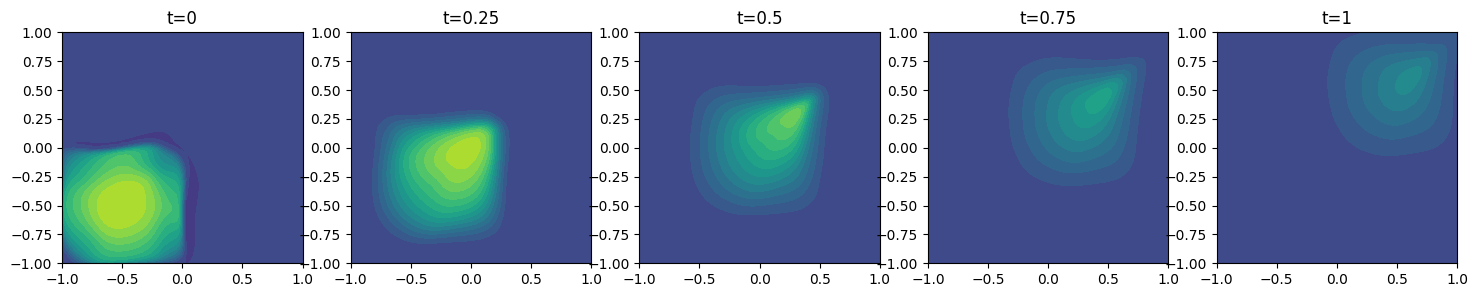
モデルから予測された速度ベクトル(u, v)の絶対値を可視化しています。期待通り,分布が少しずつ拡散しながら右上に進行している様子が描かれます。
まとめ
PINNによるバーガース方程式の予測を2次元に拡張しました。次回は,NS式へ拡張するか,物体境界の再現にトライしてみたいと思います。