Mar 4, 2024

PytorchでPhysics-Informed Neural Networkを実装する ①バーガース方程式

Pytorch

機械学習

概要

PINN(Physics-Informed Neural Network)について学習したことをまとめます。
すでに様々なところで先人が取り組まれており，以下のサイトを参考にさせていただきました。

https://www.ntt-at.co.jp/product/aicolumnlist/202303.html
https://masao-ds.hatenablog.com/entry/2023/07/09/172343
https://github.com/erfanhamdi/pinn-torch

PINNとは

通常のNN(Neural Network)では，大量の教師データを用意して，モデル出力が教師データと一致するように重みを最適化していきます。

ただし，この学習方法は教師データが存在する入力変数の範囲で誤差を最小化しているだけで，データが存在しない範囲ではどれだけモデルが極端な挙動をしたとしても制御することは難しいです。そこで，教師データへの当てはまりだけでなく，データの生成ロジック(支配方程式)に対する当てはまりも評価するように学習方法を改良したものがPINNです。

PINNの学習には以下の2つのデータが必要になります。

初期条件・境界条件を定義するデータ
支配方程式とモデル出力との一致を評価するデータ

1.は(時間, 空間座標, 物理量)といった形式になり，記号(t, x, u)で表します。このデータは通常のNNの仕組みと同様，モデル出力との誤差をとるための教師データとして扱います。

2.がPINNならではのデータで，(時間, 空間座標)の形式になっており，物理量uが含まれていません。物理量をあらかじめ教師データとして与えるのではなく，学習途中でモデルが吐き出す物理量uをもとに支配方程式の残差を計算します。つまり，教師データとの一致を見つつも，支配方程式にも適合するような物理量を出力するように学習が行われます。

コード

パッケージのインポート

必要パッケージをインストールします。モデルの中身まで細かく定義する必要があるので，今回はpytorchを用います。

pinn_burgers.ipynb

import random
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn

def torch_fix_seed(seed=42):
    """ 乱数シードを固定
    """
    random.seed(seed)
    np.random.seed(seed)
    torch.manual_seed(seed)
    torch.cuda.manual_seed(seed)
    torch.backends.cudnn.deterministic = True
    torch.use_deterministic_algorithms = True

torch_fix_seed()

データセットの作成

境界条件(初期条件，固定壁条件)に沿ったデータをそれぞれ100件ずつ作成します。
時間tと空間座標xは乱数で生成します。物理量uは初期条件の場合はsin関数，固定壁条件の場合は0を埋め込んでいます。

支配方程式の残差の評価には，乱数で生成した5000点を用います。

pinn_burgers.ipynb

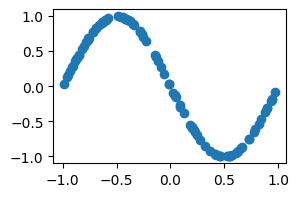
# 初期条件: x∈[-1,1], t=0のとき，u=-sin(x)
n_initial = 100
t_initial = np.zeros(n_initial) 
x_initial = (np.random.random(n_initial) - 0.5) * 2 
u_initial = -1 * np.sin(np.pi * x_initial)

# 固定壁条件: x=-1 or x=1, t∈[0,1]のとき，u=0
n_boundary = 100
t_boundary = np.random.random(n_boundary)
x_boundary = np.random.choice([-1, 1], n_boundary)
u_boundary = np.zeros(n_boundary)

# 支配方程式の残差を評価する計算領域内の座標: x∈[-1,1], t∈[0,1]
n_region = 5000
t_region = np.random.random(n_region)
x_region = (np.random.random(n_region)- 0.5) * 2 

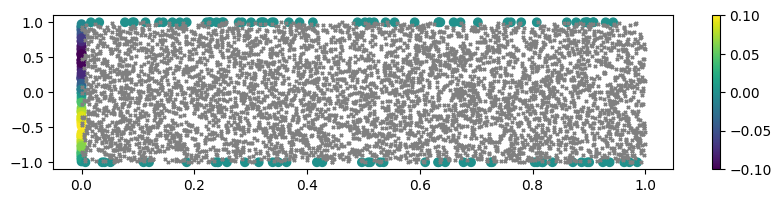
# 可視化
plt.figure(figsize=(10, 2))
plt.scatter(t_initial, x_initial, c=u_initial)
plt.scatter(t_boundary, x_boundary, c=u_boundary)
plt.colorbar()
plt.scatter(t_region, x_region, c="gray", s=5, marker="x")
plt.show()

plt.figure(figsize=(3, 2))
plt.scatter(x_initial, u_initial)
plt.show()

vis_dataset
vis_initialcondition

モデルの作成

モデルを定義します。NNクラスは一般的なニューラルネットワークです。これをBurgersPINNクラスのイニシャライザに渡すことで，Physics-Informedな学習ができるようになります。

pinn_burgers.ipynb

class NN(nn.Module):
    def __init__(self, n_input, n_output, n_hiddens=[32,64,128,128,64,32]):

        super(NN, self).__init__()
        
        self.activation = nn.Tanh()
        
        self.input_layer = nn.Linear(n_input, n_hiddens[0])
        self.hidden_layers = nn.ModuleList(
            [nn.Linear(n_hiddens[i], n_hiddens[i+1]) for i in range(len(n_hiddens)-1)]
        )
        self.output_layer = nn.Linear(n_hiddens[-1], n_output)
        
        
    def forward(self, x):
        
        x = self.activation(self.input_layer(x))
        
        for layer in self.hidden_layers:
            x = self.activation(layer(x))
        
        x = self.output_layer(x)
        
        return x


class BurgersPINN():
    def __init__(self, model):
        """ 
        """
        self.model = model
        self.nu = 0.1
        
        
    def net_u(self, x, t):
        """ 物理量を出力
        """
        u = self.model(torch.cat([x, t], dim=1))
        return u


    def net_f(self, x, t):
        """ 支配方程式との残差を出力
        """    
        # モデルが予測する物理量
        u = self.net_u(x, t)
        
        # 微分係数を逆伝搬で計算
        du_dt = torch.autograd.grad(u, t, grad_outputs=torch.ones_like(u), retain_graph=True, create_graph=True)[0]
        du_dx = torch.autograd.grad(u, x, grad_outputs=torch.ones_like(u), retain_graph=True, create_graph=True)[0]
        du_dxx = torch.autograd.grad(du_dx, x, grad_outputs=torch.ones_like(du_dx), retain_graph=True, create_graph=True)[0]
        
        # 支配方程式に代入(f=0だと方程式と完全一致)
        f = du_dt + u * du_dx - self.nu * du_dxx 
        
        return f
    
    
    def fit(self, X_bc, Y_bc, X_region, max_epochs=300, learning_rate=0.01, pi_weight=5e-4):
        """ 学習データでモデルを訓練
        """
        # 入力データをスライス
        t = X_bc[:, [0]]
        x = X_bc[:, [1]]
        u = Y_bc 
        t_region = X_region[:, [0]] 
        x_region = X_region[:, [1]]
        
        # 入力をtorch.tensorに変換
        t = torch.tensor(t, requires_grad=True).float()
        x = torch.tensor(x, requires_grad=True).float()
        u = torch.tensor(u, requires_grad=True).float()
        x_region = torch.tensor(x_region, requires_grad=True).float()
        t_region = torch.tensor(t_region, requires_grad=True).float()
        
        # 最適化ロジック
        optimizer = torch.optim.Adam(self.model.parameters(), lr=learning_rate)
        
        # モデルを学習モードに変更
        self.model.train()
        
        # 学習
        history = []
        for epoch in range(max_epochs+1):
            
            # 現在のモデルで予測
            u_pred = self.net_u(x, t)
            f_pred = self.net_f(x_region, t_region)
            
            # 損失を計算
            loss_u = torch.mean((u - u_pred)**2)
            loss_pi = torch.mean(f_pred**2)
            loss_total = loss_u + loss_pi * pi_weight
            
            # 誤差逆伝搬
            loss_total.backward()
            
            # 最適化ソルバーで重みを動かす
            optimizer.step()
            
            # 最適化ソルバーの勾配情報を初期化
            optimizer.zero_grad()
            
            if epoch % 100 == 0:
                print(f'epoch:{epoch}, loss:{loss_total.item()}, loss_u:{loss_u.item()}, loss_pi:{loss_pi.item()}')
            
                history.append([epoch, loss_total.item(), loss_u.item(), loss_pi.item()])
        
        return np.array(history)
                
    def predict(self, X_in):
        """ モデルの予測
        """
        t = X_in[:, [0]]
        x = X_in[:, [1]]
        
        # 入力をtorch.tensorに変換
        t = torch.tensor(t, requires_grad=True).float()
        x = torch.tensor(x, requires_grad=True).float()
        
        self.model.eval()  # 評価モードに変更

        u = self.net_u(x, t).detach().numpy()
        f = self.net_f(x, t).detach().numpy()
        
        return u, f

特に重要なのはBurgersPINN内のfit()関数の以下の部分です。通常のNNでは教師データのuとモデル出力u_predから損失関数を計算しますが，ここではloss_piという項が追加されています。
これが，モデル出力から計算した支配方程式の残差となります。

fit()

    # 現在のモデルで予測
    u_pred = self.net_u(x, t)
    f_pred = self.net_f(x_region, t_region)
    # 損失を計算
    loss_u = torch.mean((u - u_pred)**2)
    loss_pi = torch.mean(f_pred**2)
    loss_total = loss_u + loss_pi * pi_weight

支配方程式の残差はnet_f関数によって計算されます。ここが面白いポイントで，pytorchの自動微分機能(auto_grad)を使うことで，x，t，u等の変数同士の微分が簡単に計算できます。

通常このような非線形式は厳密解がないものも多く，解くためにかなり緻密な変換を要する(今回挙げているバーガース方程式も「コール・ホップ変換」というものが必要となる)のですが，NN内で物理量を処理することでこのような恩恵が得られます。

net_f()

    # 微分係数を逆伝搬で計算
    du_dt = torch.autograd.grad(u, t, grad_outputs=torch.ones_like(u), retain_graph=True, create_graph=True)[0]
    du_dx = torch.autograd.grad(u, x, grad_outputs=torch.ones_like(u), retain_graph=True, create_graph=True)[0]
    du_dxx = torch.autograd.grad(du_dx, x, grad_outputs=torch.ones_like(du_dx), retain_graph=True, create_graph=True)[0]
    
    # 支配方程式に代入(f=0だと方程式と完全一致)
    f = du_dt + u * du_dx - self.nu * du_dxx

学習

1000エポック分の学習を行います。

pinn_burgers.ipynb

# 学習用のデータ
X_bc = np.block([[t_initial, t_boundary], [x_initial, x_boundary]]).T
Y_bc = np.block([[u_initial, u_boundary]]).T
X_region = np.block([[t_region], [x_region]]).T

print("shape:", X_bc.shape, Y_bc.shape, X_region.shape)

model = NN(2, 1)
pinn_model = BurgersPINN(model)

# モデルを学習
history = pinn_model.fit(X_bc, Y_bc, X_region, max_epochs=1000)

# 履歴
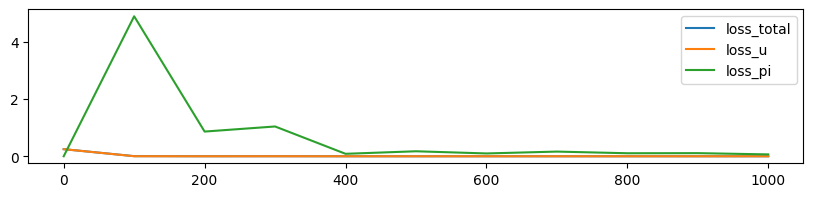
plt.figure(figsize=(10,2))
plt.plot(history[:, 0], history[:, 1], label='loss_total')
plt.plot(history[:, 0], history[:, 2], label='loss_u')
plt.plot(history[:, 0], history[:, 3], label='loss_pi')
plt.legend()

loss_uに比べてloss_piのオーダーが大きすぎるかもしれません。ここはパラメータの調整次第かなと思います。
(ミニバッチ学習になっていないため，データセットによっては局所解にはまってしまうようです...)
residuals

予測

物理量uと支配方程式の残差fを可視化します。

pinn_burgers.ipynb

# 予測したいポイント
n = 100
t_pred = np.linspace(0, 1, n)
x_pred = np.linspace(-1, 1, n)
t_grid, x_grid = np.meshgrid(t_pred, x_pred)

X_in = np.block([[t_grid.flatten()], [x_grid.flatten()]]).T

# 予測
u_pred, f_pred = pinn_model.predict(X_in)
u_pred = u_pred.reshape(n, n)
f_pred = f_pred.reshape(n, n)

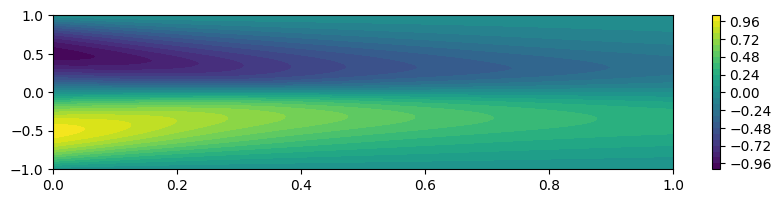
# 物理量を可視化
plt.figure(figsize=(10, 2))
plt.contourf(t_pred, x_pred, u_pred, 32)
plt.colorbar()
plt.show()

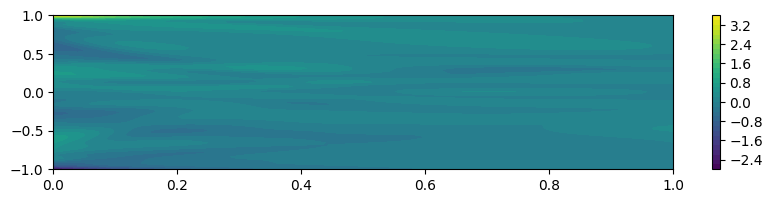
# 基礎方程式の残差を可視化
plt.figure(figsize=(10, 2))
plt.contourf(t_pred, x_pred, f_pred, 32)
plt.colorbar()
plt.show()

期待通り，全領域で残差fが0に近づき，物理量uの分布も支配方程式に沿ったものになっています。

predict_u
predict_f

pinn_burgers.ipynb

times = [0, 0.25, 0.5, 0.75]

fig = plt.figure(figsize=(15, 2))

for i, t in enumerate(times):
    t_pred = np.ones([100, 1]) * t
    X_in = np.column_stack([t_pred, x_pred])
    u_pred, f_pred = pinn_model.predict(X_in)
    
    fig.add_subplot(1, 4, i+1)    
    plt.plot(x_pred, u_pred, label='u_pred')
    plt.plot(x_pred, f_pred, label='f_pred')
    plt.ylim(-1.5, 1.5)
    plt.legend()
plt.show()

時間tを0, 0.25, 0.5, 0.75に固定して，物理量uと残差fをプロットしました。
vis_slice

まとめ

PINNの基本としてバーガース方程式の検討を行いました。
次は，より高度な支配方程式に基づいたモデルにチャレンジしたいと思います。

雰囲気データサイエンティストの備忘録

Atmosphere Data Scientist's Memorandum

概要

PINNとは

コード

パッケージのインポート

データセットの作成

モデルの作成

学習

予測

まとめ